DeVeny Pickup Noise Scrubber

Status: Beta Testing

To report problems or suggest improvements, please submit a GitHub Issue and/or Pull Request. Please include the appropriate QA plot in your Issue/PR to illustrate the problem you encountered.

Overview

The spectral channel CCD of the DeVeny Optical Spectrograph has been subject to ground-loop EMI pickup in the readout electronics during most of its tenure at the Lowell Discovery Telescope (LDT). This pickup manifests in the science images as a low-amplitude sinusoidal pattern sitting atop the raw 2D spectral image.

In January 2018, the Instrument Group broke a significant ground loop, eliminating a prominent “corduroy” noise pattern with amplitude \(\pm 4\) DN that had been affecting observers’ low-SNR extractions. At that point, there still remained a low-level (\(\pm 2\) DN) scalloping noise that shifted from frame to frame, indicating another source of EMI. After this brief reprieve, however, changes on the LDT instrument cube led to the reappearance of the larger \(\pm 4\) DN “corduroy” pattern with that continues into 2023. While the Instrument Group works diligently to identify and remove this ground loop, the present tool is available for observers whose low-SNR extractions are affected by this pickup signal.

Raw DeVeny frame with sinusoidal pickup noise

Fig. 8 – Raw frame from DeVeny taken in late 2022. This is the frame for which we will show the scrubber processing steps in the sections below. The object is the thin horizontal line in the center of the frame, and there are several prominent (vertical) night sky lines in addition to the wavy pattern caused by AC EMI pickup in the readout electronics of the CCD.

Fitting and removing the sinusoidal signal seen in Fig. 8 is complicated by the presence of bright features in the raw frame such as the observed object(s), night sky lines, and cosmic rays. We use the spectroscopic data reduction pipeline (PypeIt) with a particular set of parameters to mask cosmic rays and extract night sky lines and object spectra. With these bright signals removed, we can then to fit sinusoids to the residual noise image to produce a pattern image representing the EMI signal. This patten is then subtracted from the original image and saved to a FITS file for usual data reduction processing (preferably with PypeIt) to yield an extracted 1D spectrum for analysis.

Example Pre- and Post-Scrubbed Data Products

To illustrate the need for and utility of this tool, Fig. 9 shows a comparison of the extracted 1D spectra for two different object types from two different programs (and nights) from both the original and scrubbed version of the frame. The galaxy is the (horizontal) object in the middle of Fig. 8. Not only does this tool remove the sinusoidal oscillation in the continuum, but astrophysical measurements are more accurately measured from the spectra.

Comparison of raw and scrubbed extracted 1D spectra

Fig. 9 – Comparison of the PypeIt-extracted 1D spectra for two different object types (from different programs). For each object, the raw and scrubbed frames are shown to illustrate the utility of this tool. The red dashed line represents the \(1\sigma\) uncertainty in the spectrum. PypeIt estimates a mean \(SNR = 4.8\) for the scrubbed galaxy spectrum and a mean \(SNR = 7.2\) for the scrubbed white dwarf spectrum.

Of equivalent interest to the quality of the extracted spectra is the noise remaining after extraction of sky and objects. Shown in Fig. 10 are the noise analysis plots from PyepIt for the pre- and post-scrubbed versions of the 2D spectral image shown in Fig. 8. The images and pixel histograms are of the residual noise image, which is the science image minus the object and sky models, and then divided by the uncertainty image. The ideal pixel histogram would be a gaussian with width \(\sigma=1\).

Pre-scrubbed noise analysis plot
Post-scrubbed noise analysis plot

Fig. 10 – Noise analysis of the pre- (top) and post-scrubbed (bottom) versions of the frame shown in Fig. 8. Image values are residual image divided by uncertainty, so the ideal pixel histogram would be a gaussian with width \(\sigma=1\). Note the improvement in both the visual quality of the scrubbed frame and the width and shape of the pixel histogram compared to the pre-scrubbed frame.

Outline

This document begins with a description of how to use this tool to clean the EMI pickup noise from your data, and moves on to lay out the details of what the tool does to your data and other points to consider.

Data Processing Steps

  1. Before the pickup noise may be fit out, it is necessary to perform a basic spectroscopic reduction using the PypeIt pipeline. The outline of how to perform this reduction is given in the DeVeny User Manual. What is needed for this tool, however, is not a completely normal reduction procedure, and it is important to not modify any of the object finding, sky subtraction, or extraction parameters (except as enumerated below) in your PypeIt Reduction File for this step. The scrubber tool expects certain qualities of the processed images in order to successfully fit the EMI noise.

    In particular, to perform a sky subtraction in a way to limit the number and severity of artifacts introduced into the residual noise image and to not spend time computing spectral flexure, the user should include the following in the Parameter Block of the .pypeit file:

    [flexure]
   spec_method = skip
[reduce]
   [[skysub]]
      bspline_spacing = 100
      local_maskwidth = 200.
      no_poly = True

    Warning

    If you are using a version of PypeIt < 1.15.0 (see the top line of the PypeIt Reduction File for the version number), then you will instead need to add the entirety of the following to the Parameter Block to ensure the traced slit edges do not shrink unreasonably and that pattern noise in the CCD overscan does not introduce artifacts in the fitting. Regions outside the marked slits will have 0 value in the residual image, and therefore any sinusoidal signal there will not be fit out. (The additional parameters included here were added to the DeVeny default set in PypeIt version 1.15.0.)

    [flexure]
   spec_method = skip
[reduce]
   [[skysub]]
      bspline_spacing = 100
      local_maskwidth = 200.
      no_poly = True
   [[findobj]]
      find_trim_edge = 0,0
[calibrations]
   [[slitedges]]
      minimum_slit_length = 170
      max_nudge = 5
      det_buffer = 0
   [[flatfield]]
      tweak_slits = False
[scienceframe]
   [[process]]
      overscan_method = polynomial
      overscan_par = 1,0,0

  2. Once the PypeIt reduction is complete, you are ready to run the scrubber. In the directory containing the raw files, run the scrubber (see Usage) on the files in the directory. If an input file is NOT an object science frame (e.g., it is a bias or dome flat), it will be skipped without being processed. The scrubber will use both the raw frame and the processed 2D spectrum (in the ldt_deveny_?/Science directory) to fit the sinusoidal pickup noise and produce a cleaned image, saved to a FITS file in the raw directory.

  3. After the scrubber has completed its work, you will need to perform a normal PypeIt data reduction workflow, starting with the pypeit_setup script to include the scrubbed files in a new PypeIt Reduction File. At this point, you may remove the lines in the .pypeit file corresponding to the original images and add any parameter modifications you desire, including those affecting object finding and extraction. In particular, DO NOT include the [flexure] and three [[skysub]] parameters used in Step #1 above, as they may cause unpleasant artifacts in the actual reduction of your data.

Note

In a future version of this tool, it may be possible to combine steps #1 and #2, so that the user need not concern themselves with the particular PypeIt parameter modifications here, and would only need run this tool on the raw data (which will include an integral PypeIt reduction) before running the usual PypeIt reduction steps.

Usage

Command Line

The tool usage can be displayed by calling the script with the -h option:

$ scrub_deveny_pickup -h
usage: scrub_deveny_pickup [-h] [--proc_dir PROC_DIR] [--overwrite_raw] [-d]
                           [-n]
                           file [file ...]

Clean RF pickup noise from DeVeny raw frames

positional arguments:
  file                 File(s) to clean

options:
  -h, --help           show this help message and exit
  --proc_dir PROC_DIR  Path to the directory above that which contains the
                       .pypeit file used to process `file` (i.e., the directory
                       above ldt_deveny_?) -- use only if `-r` was used in the
                       call to `pypeit_setup`. (default: current working
                       directory)
  --overwrite_raw      Overwrite the raw file rather than create a new file with
                       the '_scrub' suffix (default: False)
  -d, --diagnostics    Output additional information and plots during the
                       analysis for debugging purposes (default: False)
  -n, --no_refit       Force no refit of 'bad' RMS values (default: False)

You may specify either a single file for the scrubber to process, or include a list of files (by way of wildcards or shell filename expansions) over which the tool should iterate.

The --proc_dir option may be used to specify the location of the PypeIt-processed files (i.e., the ldt_deveny_? directory you created with pypeit_setup), if other than as a subdirectory of the raw data directory. This works in the same sense but opposite direction as the -r <RAWDIR> option to pypeit_setup. In particular, if you did not specify -r <RAWDIR> to pypeit_setup, do not use this option.

To simply overwrite the raw data file with the output of this tool, the --overwrite_raw option may be specified. Since the output FITS file created here includes the entirety of the raw frame (all header cards plus the raw image), this may be acceptable if processing large number of files.

Other options shown are debugging tools that may be removed in the future.

Terminal Output

When run, the tool prints to the screen information about the current processing step and produces progress bars when repeatedly running an algorithm on multiple rows of the image. The terminal output for the example frame used in this documentation is shown below.

$ scrub_deveny_pickup 20290101.0001.fits

Processing frame 20290101.0001.fits
--> FFT-predicted pixel period: 169.7 pix
Checking the object model for bulk sinusoidal signal...
100%|██████████████████████████████████████████| 46/46 [00:01<00:00, 23.84row/s]
* Object model appears clean of target sinusoidal signal.
Fitting sinusoids to each line in the image...
100%|████████████████████████████████████████| 508/508 [00:10<00:00, 50.45row/s]
   --> Mean fit pixel period: 172.9 pix
Refitting lines with poor fit in first pass...
100%|██████████████████████████████████████████| 63/63 [00:01<00:00, 50.86row/s]
   --> Mean fit pixel period: 173.7 pix
Refitting all lines within the slit assuming nearly constant sinusoid...
100%|████████████████████████████████████████| 478/478 [00:07<00:00, 62.00row/s]
   --> Mean fit pixel period: 173.7 pix
 Writing QA plots to ./ldt_deveny_A/QA/PDFs
Writing out scrubbed FITS file: 20290101.0001_scrub.fits

Important pieces to note in the terminal output:

  • The FFT-predicted and mean sinusoid fit pixel periods are printed for quality assurance purposes.

  • If the PypeIt-reduced spec2d file contains a non-zero object model, the code will analyze it for the sinusoidal signal at the predicted period. If the object model contains this signal, then the residual noise image (sciimg - skymodel - objmodel) will be missing power from the pickup noise (i.e., that power was extracted into the object model). In this case, the tool will print a statement indicating that the object model will be included in the residual image and the amplitude of the sinusoidal fit (for QA purposes). If the object(s) remains extracted (i.e. does not contain bulk sinusoidal signal), the tool will print the message: Object model appears clean of target sinusoidal signal.

  • The first pass at fitting sinusoids to the image should include all rows in the (trimmed) image (FITS keyword TRIMSEC). In this example, the CCD was binned 1x1, so there were 516 rows in the original image, trimmed down to 508.

  • As an iterative step, the tool assesses the rms residuals of the fit and determines if there are outliers that need to be refit using initial guess parameters from nearby well-fit rows. The number of rows indicated in this progress bar is less than the total image, and can vary based on the particular pattern noise in the image.

  • The EMI signal should be roughly constant in amplitude and period over the approximately 8 seconds the CCD takes to read out. Therefore, as a final step, the tool fits the amplitude and period fit coefficients with a low-order polynomial as a function of row number to account for the secular drift in the sinusoid period that causes the mean period to change from frame to frame. With the polynomial fit in hand, one last pass at fitting sinusoids to the rows is completed, fixing the period and amplitude while allowing the phase and underlying secular drift of the row to be fit. This pass only fits rows identified within the slit, so may have fewer rows to process than the full frame.

  • Finally, the location of QA plots and filename of the scrubbed FITS file are shown for reference.

Output FITS File

The output of this tool is a multiextension FITS with filename identical to the raw file (including path) except with “_scrub” appended before “.fits”. It includes the following HDUs:

  • Primary HDU: contains the raw file’s complete FITS header

  • Cleaned Image HDU: (raw - pattern)

  • Original Image HDU: (raw)

  • Pattern Image HDU: (pattern)

  • Pattern about Raw Mean Image HDU: (pattern + mean(raw))

  • Fit Coefficients BinTable HDU: (fit_coeffs)

Running the AstroPy utility fitsinfo yields the following:

$ fitsinfo 20290101.0001_scrub.fits
Filename: 20290101.0001_scrub.fits
No.    Name      Ver    Type      Cards   Dimensions   Format
  0  PRIMARY       1 PrimaryHDU     193   ()
  1  CLEANED       1 ImageHDU        10   (2148, 516)   float64
  2  ORIGINAL      1 ImageHDU        12   (2148, 516)   int16 (rescales to uint16)
  3  PATTERN0      1 ImageHDU        10   (2148, 516)   float64
  4  PATTERN1      1 ImageHDU        10   (2148, 516)   float64
  5  FIT DATA      1 BinTableHDU     50   508R x 15C   [D, D, D, D, D, D, D, D, D, D, D, D, D, D, D]

The ORIGINAL raw data frame is included in the scrubbed output for reference and posterity. The fitted sinusoidal pattern is included in two different formats, one with a zero mean (PATTERN0) and the other with the raw image mean (PATTERN1) for use as desired (e.g. it is easier to compare PATTERN1 to the raw image in ds9, but the actual signal removed from the raw image is PATTERN0). Finally, the sinusoidal fit coefficients are included for perusal.

When processing the scrubbed frames with PypeIt, the data reduction pipeline will recognize the scrubbed image and use the CLEANED HDU for processing without user intervention.

QA Plots

The tool generates three quality assurance (QA) plots per frame to allow the user to assess the scrubbing. All QA plots are placed into the PypeIt QA/ directory for convenience. Within the PypeIt QA/ directory, that pipeline places its QA plots into a PNGs/ subdirectory (because the plots are PNG format). To keep QA files from this tool separate (yet also in an easy-to-find location), files generated here are in the PDFs/ subdirectory (because, wait for it, they are in PDF format).

The three files are:

  1. The FFT QA plots showing the frequencies found and indicating the likely period of the EMI noise. (See Fig. 11 as an example.) These have the filename template YYYYMMDD.NNNN_scrubber_fft_analysis.pdf where the YYYYMMDD.NNNN corresponds to the filename of the raw frame.

  2. The sinusoidal fits QA plots showing the row-by-row fit coefficients and rms residuals. (See Fig. 12 as an example.) These have the filename template YYYYMMDD.NNNN_scrubber_sinusoid_fits.pdf.

  3. Image comparison QA plots showing the various stages of the analysis including the original (PypeIt-processed) frame, residual image, modeled pattern noise, and cleaned image. (See Fig. 13 as an example.) These have the filename template YYYYMMDD.NNNN_scrubber_image_comparisons.pdf.

Algorithmic Details of the Scrubbing

Here we describe the processing details for the scrubber and illustrate example QA plots generated by the tool.

The fitting of the sinusoidal pickup noise is done on the residual PypeIt-processed image, in which cosmic rays, the sky model, and (frequently) the object have been removed, leaving behind the underlying noise in the image. This is done because bright features in the raw science frame such as night sky lines and objects obfuscate and cover the few-DN amplitude AC signal we wish to remove. We take advantage of the sophisticated modeling algorithms in PypeIt to do this heavy lifting for us, leaving us to concentrate on the DeVeny-specific issues at hand. See Fig. 13 below for an illustration of the various processing steps and frames used.

Important

PypeIt converts all raw images from ADU into electrons using the gain value recorded in the FITS header. For DeVeny, this is 1.52 e-/ADU. The QA plots shown here are constructed from the PypeIt-processed images, and so are in electrons. The \(\pm 6\) electron amplitude illustrated here translates to a \(\pm 4\) DN signal in the raw images.

Note

Include a description of when the object may or may not be included in the residual image – namely if the object model from PypeIt contains sinusoidal signal of the period indicated from the FFT.

FFT Analysis

The EMI pickup noise present in the DeVeny images has an unpredictably variable apparent frequency (or wavelength in pixel space) from frame to frame. The secular variation in the frequency is slow enough, however, that the measured wavelength of the sinusoidal noise is approximately constant across a single image given the \(\sim 8\) second readout time of the spectral channel CCD.

Estimation of the mean sinusoid period is done with a fast fourier transform (FFT). Rather than attempt to pull the (varying) horizontal frequencies out of a 2D FFT, the image is instead flattened into a timeseries-like array, where pixels are arranged in the order in which they were read out. In its processing, PypeIt trims the raw image to remove overscan sections and unruly rows at the edges of the CCD. As such, the last pixel of one row is not strictly temporally adjacent to the first pixel of the next row in the same way that pixels within a given row are. Rather than attempt to fill in a temporally appropriate gap between rows (which would introduce artifacts in the resulting FFT), we simply stitch the rows together as-is and rely upon the FFT to pick out the prominent frequencies in the flattened array.

An example QA plot for the FFT analysis is shown in Fig. 11.

FFT analysis of the flattened frame

Fig. 11 – FFT QA plot. The top panel shows the flattened image array, while the remaining rows show the real (amplitude as a function of frequency), imaginary (phase as a function of frequency), and absolute square (power spectrum) components of the FFT. The power spectrum is further smoothed with a gaussian kernel to help isolate desired signal (with variable frequency, as discussed above) from artifacts and ringing in the FFT. The peak at 169.7 pixels indicates the frequency with the most power in the flattened array: most likely the period of the AC EMI pickup noise.

The power spectrum of the FFT (absolute value squared) is smoothed with a 10-Hz wide gaussian kernel since there is variation in the frequency of the sinusoid from row to row. This has the added benefit of squashing artificial peaks in the power spectrum caused by ringing or aliasing of the signal across rows. We use the pixel period of the peak of the power spectrum as the initial guess for the iterative fitting of a sinusoid (in pixel space) to each row of the residual image.

Row-by-Row Sinusoid Fits

With an initial guess at the sinusoid period in hand, the tool moves on to fit a sinusoid to each row in the image. This is an iterative process, where the results of one pass inform the initial guess and bounds on the fit parameters for subsequent passes. In addition to a basic sinusoid (amplitude, period, and phase), a quadratic polynomial is included to account for secular drift in the background. The curve_fit() function from scipy.optimize is used to perform a non-linear least-squares fit to each row, with bounds placed on the sinusoid terms to keep the final fit reasonably close to initial guess values.

Fig. 12 shows the result of this iterative fitting for this example frame. During each pass, the rms of the fit is computed for each row as an estimate of how well any particular row’s model matches the data. The mean and standard deviation of the row-by-row rms values (bottom panel in Fig. 12) are used to identify outliers that likely have a poor fit after the first pass.

In the second pass, these outlier lines are refit with tighter bounds and using the fit values from nearby “good” rows as the initial guesses. The collection of fit values as a function of row number after the second pass are shown in orange in Fig. 12. As a result of this iterative process, the set of sinusoidal fits tends to have a narrow range of values for amplitude and period.

For the final pass, the tool assumes that the underlying EMI noise is nearly constant in period and amplitude. A low-order (quadratic) polynomial is fit to the top two plots in Fig. 12 to estimate the true sinusoidal signal imprinted on the frame. The sinusoidal fits for this pass fix the values of the period and amplitude to those smooth values (black lines in Fig. 12), allowing the phase and secular drift of the row to be fit. As a result, the sinusoid phase from row to row is a smoother function, and the rms of the fit is generally a little smaller than the orange fit.

The pattern image produced from these final fit coefficients (see Fig. 13) closely resembles the unwanted pattern in the raw frame. Note, however, that the final pixel periods tend to be slightly larger than that predicted from the FFT (green dashed line in the second panel of Fig. 12). The origin of this discrepancy is not clear (see Line-by-Line Fits vs Fourier-Space Filtering for further discussion).

Sinusoid fits to each row

Fig. 12 – Sinusoid fit QA plots, showing the row-by-row fit parameters for the amplitude, period, and phase in the first three panels, and the rms of the fit in the bottom panel. In the period panel, the green dashed line indicates the peak of the FFT power spectrum used as the initial guess for the sinusoid fit parameters.

Pickup Noise Pattern Construction

The final result of sinusoid fits is a constructed pattern image. This is the zero-mean sinusoid (sans quadratic polynomial) that should represent only the EMI pickup noise (as an additive AC-only signal). Fig. 13 shows the process of pattern construction and its effect on the processed science image.

Image comparison plot showing initial, intermediate, and final images

Fig. 13 – This QA plot illustrates the image-space effects of the sinusoidal fits. Panels are all shown with the IRAF ZScale mapping; panels sharing a color map also share visualization scale limits. The panels are described below.

Panel Description:

  1. The science image after the initial PypeIt processing. Without scrubbing, this would be the 2D image from which the object(s) are extracted.

  2. The PypeIt sky + object model, where the local sky modeling has included the entire slit thanks to the local_maskwidth = 200. specified in the PypeIt Reduction File. If the object is not included here, it is because the extracted object model includes power from the sinusoidal EMI signal and must therefore be included in the residual image for fitting. The sky is purposefully broad-brush and blurred so as to not induce artifacts in the fitted pattern by including, e.g., contiguous rows of sinusoids with similar phase in the sky model (rather in the noise pattern where it belongs).

  3. The PypeIt residual image, where the sky model (and frequently the object model) has been subtracted and cosmic rays (and other bad pixels) have been masked. What should remain in this image is flat residual noise with rms based on the sky model photon statistics. In the case of DeVeny images subject to the EMI pickup noise, that noise should be the dominant feature in this frame, with some residual sky lines because of the broad-brush sky subtraction above.

  4. The modeled sinusoidal pickup noise. While the sinusoidal fit to each row of the residual image (#3) includes a quadratic polynomial to account for secular variation in the background, only the base sinusoid is included in this pattern image to match the AC nature of the pickup.

  5. The scrubbed residual image, where the pattern image (#4) has been subtracted off. This frame should be largely featureless (except if the object is still included).

  6. This is the scrubbed science frame (#1 minus #4), and it should be clear of the sinusoidal noise. Even in frames where the phase difference of the pickup noise from row to row is such that large-scale wavy patterns are not visible in the base science image (#1), this scrubbed frame should be less noisy since a \(\sim 4\) DN sinusoid has been removed from each line.

Panels #1, #2, and #6 are shown in a purple-red-yellow color map with common scale limits based on the processed science image (range -15 e- to +51 e-), and panels #3 - #5 are shown in a blue-green-yellow color map with common scale limits based on the pattern image (range -6.1 e- to +6.1 e-) to illustrate the completeness of the EMI signal removal.

Appendix

For the adventurous reader, here is some additional information about the development of the scrubber and various points of interest.

Line-by-Line Fits vs Fourier-Space Filtering

Todo

This section needs updated images and text.

Given the nearly constant frequency (manifested as a periodic sinusoid in pixel space) of the AC EMI, one is tempted to attempt filtering the signal in Fourier space rather than doing a line-by-line fitting.

The FFT computation is done on a flattened 1D version of the image, with the pixels in time-order of readout. Now, if the exact time between rows were included as spacers between the rows of data in the 1D array, a single period may emerge. Since this is difficult to guess (and can vary within the readout electronics), the rows were simply strung together one after another. The effect of this is a significant amount of ringing in the FFT caused by breaks in the sinusoidal pattern from row to row.

We can run the computed EMI pattern image (4th panel in Fig. 13) through the same FFT analysis routine to yield the QA plot shown in Fig. 14.

FFT analysis of the constructed pattern

Fig. 14 – FFT QA plot, showing the flattened image array, the real (amplitude as a function of frequency) and imaginary (phase as a function of frequency) components of the FFT, along with the power spectrum (absolute value squared). The power spectrum is further smoothed with a gaussian kernel to help isolate real signal (with variable frequency, as discussed above) from artifacts and ringing in the FFT. The peak at 169.1 pixels, indicating the frequency with the most power in the flattened array: most likely the period of the AC EMI pickup noise.

When compared to Fig. 11, most of the structure apparent in the analysis of the residual image still appears here. This is why simply applying a notch filter in Fourier space around the peak of the FFT does not clean the EMI noise, but rather amplifies the problem. It is comforting that the peak period found in the pattern image is identical to that in the residual image (169.1 pixels), although both are smaller than the average pixel period found in the sinusoid fitting (173.6 pixels).

Finally, we can perform the same analysis on the scrubbed residual image (5th panel in Fig. 13). The result is shown in Fig. 15.

FFT analysis of the cleaned residual image

Fig. 15 – FFT QA plot, showing the flattened image array, the real (amplitude as a function of frequency) and imaginary (phase as a function of frequency) components of the FFT, along with the power spectrum (absolute value squared). The power spectrum is further smoothed with a gaussian kernel to help isolate real signal (with variable frequency, as discussed above) from artifacts and ringing in the FFT. The peak at 169.1 pixels, indicating the frequency with the most power in the flattened array: most likely the period of the AC EMI pickup noise.

Also, say something about the actual line-by-line fits in terms of how good a sinusoid fits each one. Show a figure like Fig. 16.

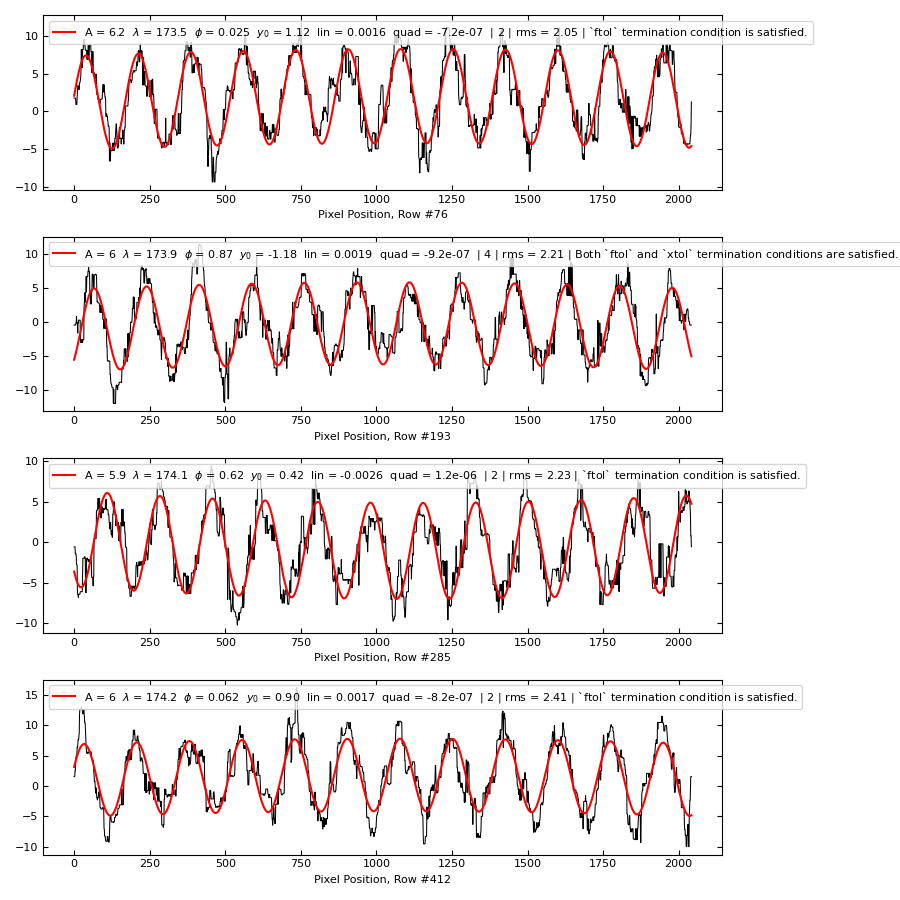
Line-by-line fitting examples

Fig. 16 – Examples of individual line fits for 4 randomly selected lines from the image shown in Fig. 8.